Fig. 7

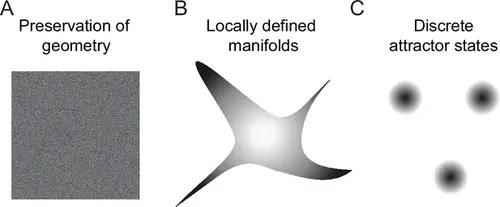
Schematic of geometric transformations. (A) Randomly connected networks tend to preserve the geometry of coding space. Such networks can support neuronal computations, for example, by projecting activity patterns in a higher-dimensional coding space for pattern classification. (B) We found that balanced networks with E/I assemblies transform the geometry of representations by locally restricting activity onto manifolds. These networks stored information about learned inputs while preserving continuity of the coding space. Such a geometry may support fast classification, continual learning and cognitive computations. Note that the true manifold geometry cannot be visualized appropriately in 2D because activity was ?focused? in different subsets of dimensions at different locations of coding space. As a consequence, the dimensionality of activity remained substantial. (C) Neuronal assemblies without precise balance established discrete attractor states, as observed in memory networks that store information as discrete items. Networks establishing locally defined activity manifolds (B) may thus be considered as intermediates between networks generating continuous representations without memories (A) and classical memory networks with discrete attractor dynamics (C).