(A) Multiple airinemes extend from xanthoblast (undifferentiated yellow pigment cell, green). Airineme makes successful contact (arrowhead) with melanophore cell (pigment cell, purple). Asterisks indicate airinemes from other sources. Scale bar: 50 µm. (B) Model schematic. A single airineme extends from the source (right, green circle) and searches for the target cell (left, purple circle). Target cell has radius rtarg and has distance dtarg away from the origin. The airineme’s contour length at time t is l⁢(t).

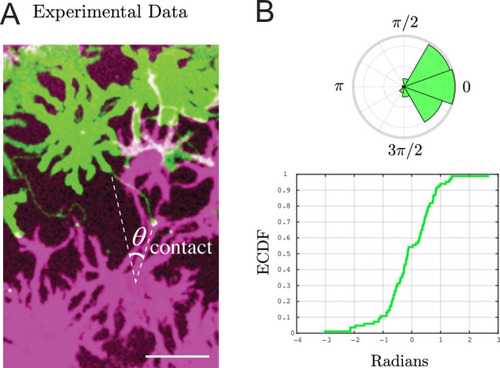
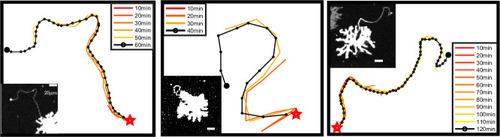
Each panel shows the examination of a single representative airineme as it emerges from the source cell at t=0, large star. Every 10 min, the shape is tracked at discrete points as it grows away from the source cell. The micrograph of the final length is shown as an inset (only the channel labeling the source cell is shown, so the target cells are not visible). Scale bar is in 20 µm. We computed root mean squared curvature of both the time-series tip location and of just the final state for the airinemes shown here. These two methods yield a difference, on average, of 0.7%. Thus, we conclude that the shape of the part of the airineme already existing at time t does not significantly change after time t as the tip of the airineme continues to extend.

Each panel shows the examination of a single representative airineme as it emerges from the source cell at t=0, large star. Every 10 min, the shape is tracked at discrete points as it grows away from the source cell. The micrograph of the final length is shown as an inset (only the channel labeling the source cell is shown, so the target cells are not visible). Scale bar is in 20 µm. We computed root mean squared curvature of both the time-series tip location and of just the final state for the airinemes shown here. These two methods yield a difference, on average, of 0.7%. Thus, we conclude that the shape of the part of the airineme already existing at time t does not significantly change after time t as the tip of the airineme continues to extend.

For the model parameter l_max, which is the length at which an airineme stops searching if it has not yet found a target, we wondered whether a single number would be appropriate or whether we needed to use a distribution to capture the variability of airineme lengths. We measure the experimental quantity l_final, which is the length of airinemes when they stop growing, whether or not they have made contact with a target cell, shown in red in (A, B) (N=56 airinemes). We run simulations in which target cells are randomly placed according to 2D Poisson statistics with mean distance dtarg=50μm and measured their length distribution when they stop growing l_final, shown in blue in (A, C) (again, whether or not they have made contact with a target). We find that the distributions for experimental data and simulated data agree qualitatively when lmax=250μm. Note that the variability in both experimental and simulated distributions is of similar magnitude, suggesting that the randomness in observed airineme length arises from the randomness in target cell placement.

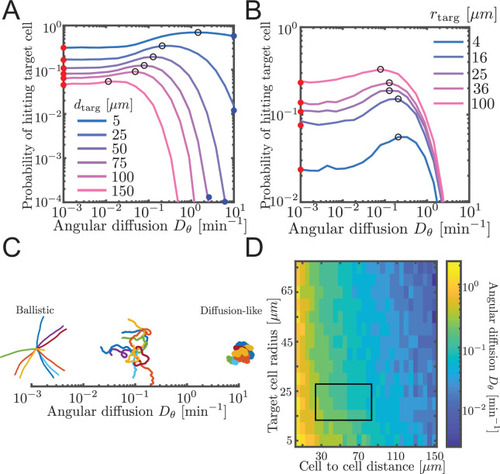
For the model parameter l_max, which is the length at which an airineme stops searching if it has not yet found a target, we wondered whether a single number would be appropriate or whether we needed to use a distribution to capture the variability of airineme lengths. We measure the experimental quantity l_final, which is the length of airinemes when they stop growing, whether or not they have made contact with a target cell, shown in red in (A, B) (N=56 airinemes). We run simulations in which target cells are randomly placed according to 2D Poisson statistics with mean distance dtarg=50μm and measured their length distribution when they stop growing l_final, shown in blue in (A, C) (again, whether or not they have made contact with a target). We find that the distributions for experimental data and simulated data agree qualitatively when lmax=250μm. Note that the variability in both experimental and simulated distributions is of similar magnitude, suggesting that the randomness in observed airineme length arises from the randomness in target cell placement.

Same as Figure 3A and B, but showing contact success as mean number of attempts (=1/pcontact).

(I) Fully extended airineme micrograph image. Arrow indicates the airineme. (II) Extraction of the average noise level from image. (III) Images of simulated airinemes are convoluted to have the same statistical noise properties of the experimental image. We use a ‘ground truth’ Dθ∼0.1525⁢min-1. (IV) In order to characterize technical variation in our analysis pipeline, five people used a manual image analysis pipeline to locate points along airinemes. From these points, curvatures and autocorrelation functions were computed, and Dθ likelihoods extracted. Curvature of simulated airineme images and likelihood distributions are shown as colored curves. Black curve shows the likelihood distribution for combined data. (V) The maximum likelihood Dθ value was close to the simulation input Dθ, with typically 2% error. The most erroneous (yellow curve) was 7% and corresponds to the manual entry of the corresponding author, JA. (Top right) Likelihoods of Dθ estimates from experimental images from five people (colored curves) and combined (black curve).

(I) Fully extended airineme micrograph image. Arrow indicates the airineme. (II) Extraction of the average noise level from image. (III) Images of simulated airinemes are convoluted to have the same statistical noise properties of the experimental image. We use a ‘ground truth’ Dθ∼0.1525⁢min-1. (IV) In order to characterize technical variation in our analysis pipeline, five people used a manual image analysis pipeline to locate points along airinemes. From these points, curvatures and autocorrelation functions were computed, and Dθ likelihoods extracted. Curvature of simulated airineme images and likelihood distributions are shown as colored curves. Black curve shows the likelihood distribution for combined data. (V) The maximum likelihood Dθ value was close to the simulation input Dθ, with typically 2% error. The most erroneous (yellow curve) was 7% and corresponds to the manual entry of the corresponding author, JA. (Top right) Likelihoods of Dθ estimates from experimental images from five people (colored curves) and combined (black curve).

(A) Representative image of source cell (green), airineme (light green, touching two white lines), and target cell (purple). To estimate the contact angle distribution, we draw a line from the source of the airineme to the center of the nucleus of the target cell, then another line from here to the airineme contact point. Scale bar is 50 μm. (B) The angle distribution of contact angles shown in an angular histogram (top) and empirical cumulative distribution (bottom). From these, compute (unmodified) Fisher information (FI) of 3.93×10-4⁢rad-2, and modified FI to be 5.7×10-5⁢rad-2 from Equation 9. Data from N=83 airinemes.

(A) Representative image of source cell (green), airineme (light green, touching two white lines), and target cell (purple). To estimate the contact angle distribution, we draw a line from the source of the airineme to the center of the nucleus of the target cell, then another line from here to the airineme contact point. Scale bar is 50 μm. (B) The angle distribution of contact angles shown in an angular histogram (top) and empirical cumulative distribution (bottom). From these, compute (unmodified) Fisher information (FI) of 3.93×10-4⁢rad-2, and modified FI to be 5.7×10-5⁢rad-2 from Equation 9. Data from N=83 airinemes.

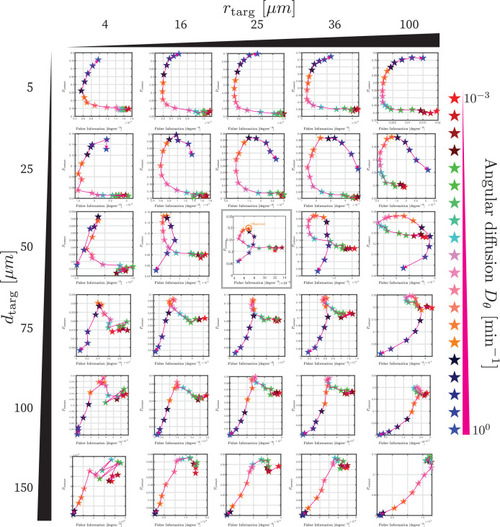
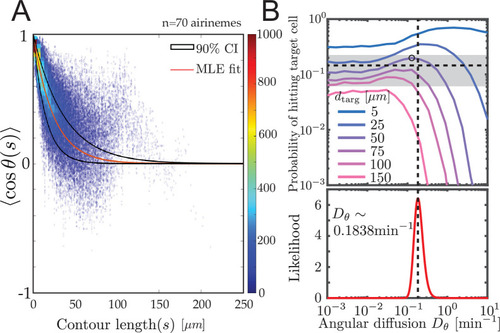
Each plot shows, identically to Figure 5D, the contact probability Pcontact (vertical axis) versus the directional information (modified Fisher information defined in Equation 9) for a range of angular diffusion coefficients Dθ indicated by color along a parametric curve. The grid of plots shows this for a range of distances to the target d_targ and target sizes r_targ. Note that although we do not explicitly explore l_max, since these plots have not been nondimensionalized, the parametric curve for a different l_max can be obtained by rescaling the results shown.